Waffle cone
This is a picture of a waffle cone. Waffle cones are typically used to hold ice cream or other sweet confections, but they have other uses, including in the construction of trigonometric proofs.
Clickbait and switch
If you’re as ignorant of the branch of mathematics known as ‘number theory’ as I was six months ago you mightn’t know that Goldbach’s Conjecture is simply that every even number greater than two is the sum of two prime numbers.
But not only is there no trigonometric proof of Goldbach’s Conjecture, there is no proof of it at all. I chose A trigonometric proof of Goldbach's Conjecture as the title for this essay as an experiment to see if it would scare up any readers from search engines. Because if there were, in fact, a trigonometric proof of Goldbach’s Conjecture — or any proof at all — it would be front-page news. This is called ‘clickbaiting,’ and it is an entirely disreputable practice.
This essay is mostly about things only tangentially related to trigonometry1, or to Goldbach’s Conjecture. It does, however discuss some other proofs — including some that resemble the one ascribed by (“[s]tately, plump”) Buck Mulligan to Stephen Dedalus in James Joyce’s Ulysses:
"He proves by algebra that Hamlet's grandson is Shakespeare's grandfather and that he himself is the ghost of his own father."
That’s the kind of algebraic logic we like to follow here in Sundman figures it out! By the time you finish reading this essay — assuming you read it well, that is, to understand — you’ll be as enlightened as any fearful Jesuit in any iconic Irish modernist novel.
Young Catholic Mathematicians
Ne'Kiya Jackson and Calcea Johnson are young mathematicians who recently graduated from St. Mary’s Academy, an all-girl and all Black Catholic high school in New Orleans. They, in fact, recently discovered a trigonometric proof which has garnered a lot of attention — it was a ‘first’ in a few categories. But their proof was not a proof of Goldbach’s Conjecture. It was a proof of a theorem much older than that.
Shifted reading frames revisited
My essay I Saw a Tangerine Sun Suspended in Haze Over the Cemetery Tonight also contained several firsts. It contains the first (and so far only) photo by Nancy Jephcote in these Sundman figures it out! essays, the first mention of books titled The Sense of an Ending (the novel by Julian Barnes; the book of literary criticism by Frank Kermode), the first mention of the poem ‘The Great Figure’ by William Carlos Williams (and the first mention of the painting ‘The figure 5 in gold’ by Charles Demuth, which was inspired by Williams’ poem). The Tangerine Sun essay also contains the first mention of the molecular biologist with the great figure.
The molecular biologist with the great figure has since been mentioned in the essays Shifted Reading Frames and How I decoded the human genome, redux, among others.
Crane before Williams
William Carlos Williams is considered an early proponent of the modernist style in poetry but Stephen Crane got there before him. Recall this little light-hearted gem that you first encountered in high school:
In the Desert
by Stephen Crane
In the desert
I saw a creature, naked, bestial,
Who, squatting upon the ground,
Held his heart in his hands,
And ate of it.
I said, “Is it good, friend?”
“It is bitter—bitter,” he answered;
“But I like it
“Because it is bitter,
“And because it is my heart.”Some people call Stephen Crane’s poetry ‘pre-modern’ or ‘proto modern’ but it sure looks modern to me. I don’t know what year ‘The Great Figure’ was written but In the Desert was published in 1895 when William Carlos Williams was only twelve years old, and Williams’s self-published book Poems did not appear until 1909, and it does not contain ‘The Great Figure.’ In fact ‘The Great Figure’ is first anthologized in Williams’ Sour Grapes in 1921, so it is nearly certain, though not proved, that ‘In the Desert’ antedates ‘The Great Figure’ by two decades, at least.
Uncle Petros pulls a fast one
The novel I’ve most recently read is Uncle Petros and Goldbach’s Conjecture(1992) by Apostolos Doxiadis (translated from the Greek by the author). I chanced upon this book while browsing Thriftbooks.com not long after I had written, in that ‘Tangerine sun’ essay, about the poem entitled ‘The Great Figure’ and ‘The number five in gold’ (and the molecular biologist with the great figure, of course).
The reproduction of Demuth’s painting ‘The number five in gold’ on the cover of Uncle Petros and Goldbach’s Conjecture really jumped out at me and the synopsis of the book provided by the publisher was intriguing so of course I had to buy a copy.
The synopsis:
Petros Papachristos, a mathematical prodigy, has devoted much of his life trying to prove one of the greatest mathematical challenges of all time: Goldbach's Conjecture, the deceptively simple claim that every even number greater than two is the sum of two primes. His feverish and singular pursuit of this goal has come to define his life. Now an old man, he is looked on with suspicion and shame by his family-until his ambitious young nephew intervenes.
When we take this book in hand, and read it well, that is, to understand, we learn, early on, that Uncle Petros has tricked his earnest nephew. He has made the nephew sign a pledge that, in exchange for the uncle’s promise to tutor him, he will renounce mathematics entirely if he cannot find a proof of the conjecture within three months.
You see, the nephew — who is the narrator of this novel — has heard of the Goldbach Conjecture, and he knows that his uncle has devoted his life trying to find a proof of it, but he does not yet know what the conjecture is.
The uncle knows that it will be virtually impossible for the boy to find such a proof, but the naive nephew doesn’t know that it is impossible, and so he sets off.
Wafflecone proof
In 2023, Ne'Kiya Jackson and Calcea Johnson announced their discovery of a trigonometric proof of the Pythagorean Theorem, which is, as you well recall, my dear child, that if you know the lengths of any two sides of a right triangle you can compute the length of the third one. Before their announcement it was widely believed that no such trigonometric proof was possible. Their story was featured recently on the TV show “60 Minutes” which you can find easily enough.
Jackson & Johnson constructed a geometric figure that they called ‘the waffle cone’ and used that figure, and trigonometry, to prove the theorem. Professional mathematicians agreed that their proof was both novel and correct. Some of them have gone on to explore their proof and derive further insights from it.
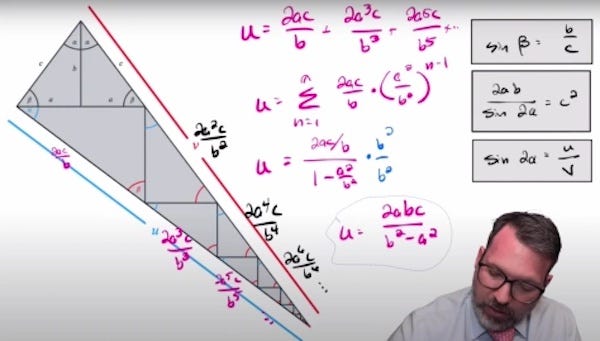
This thread on Stack Exchange in which various proofs inspired by Jackson & Johnson are discussed is representative:
There are other aspects of Ne’Kiya Jackson and Calcea Johnson's proof of Pythagoras' Theorem which I believe are more clever and interesting than its non-circular use of trigonometry. The trigonometry is a curiosity, for sure, but even more novel and intriguing connections appear through geometric and algebraic variations of their theorem, which I will present in a future answer. I still need to research how closely these variations approach any of proofs in The Pythagorean Proposition by Elisha Loomis.
I am starting here with a more straightforward and direct trigonometric proof of Pythagoras' theorem, which came to me and was inspired by the work of Jackson and Johnson. It does not require the law of sines, just the basic definitions of the sine and cosine ratios appearing in a right triangle.
In the “60 Minutes” video and elsewhere both Jackson and Johnson disclaim any deep love for mathematics, which they both call ‘hard’. Neither of them, now both college students, plan to major in math. Yet they both worked diligently for months to derive their spectacular proof.
Why?
Gödel the Nemesis
In my just prior essay Entangled I made a funny about the logician Kurt Gödel. I said
The converse to that statement (i.e. that anybody who claims they do not understand quantum mechanics does understand quantum mechanics) is not true, by the way — as may have been proved by Kurt Gödel, the logician of mathematics known for his ontological proof of the existence of God, which in many ways resembles that of Duns Scotus, the Scottish Franciscan friar and philosopher (c. 1265/66–1308).
The joke of course is that while millions of people have heard of Kurt Gödel, few of them know of his ontological proof of the existence of God, and even fewer of them care out it. Gödel is known, rather, for his incompleteness theorems. From Wikipedia:
Gödel's incompleteness theorems are two theorems of mathematical logic that are concerned with the limits of provability in formal axiomatic theories. These results, published by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics.
In the novel by Doxiadis, Uncle Petros is driven nearly to distraction by Gödel’s proof that it is possible that Goldbach’s Conjecture may be true but yet unprovable — that his entire life’s singular goal may actually be unattainable — and by Turing’s further proof that it is impossible to know a priori whether any true theorem is or isn’t provable — that is, that Petros will never know whether he failed to find a proof of the conjecture because he wasn’t brilliant enough, or because he didn’t work hard enough, or simply because the proof was, actually, unfindable.
Diligent scholars of Sundman figures it out! know well that Kurt Gödel in general, and the book Gödel, Escher, Bach: An Eternal Golden Braid by Douglas Hofstadter feature prominently in this ongoing meditation, as you can prove to yourself with some elementary sleuthing.
The halting problem and the sense of the sense of the Sense of an Ending
Turing’s result on the unknowability of the provability of any theorem is a consequence of his findings on the ‘halting problem.’ Again from Wikipedia:
In computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running, or continue to run forever.
In that Tangerine sun essay I keep steering you to, oh my most incurious one, I talked about that perfect miniature of a novel The Sense of an Ending, by Julian Barnes, and about the book of literary criticism The Sense of an Ending, by Frank Kermode. I also made reference to Will Storr’s excellent tome The Science of Storytelling.
All three of these books concern how endings — finality — whether implied or explicit, are necessary for stories to work, and, most importantly, how our own senses of our own individual endings change over time, and thus too the stories we tell ourselves about who we are.
There’s a halting problem there too, of course, in our consideration of our own particular endings, for as Jesus is said to have said,
No one knows when that day or hour will come. Even the angels in heaven don’t know,
and as Jimi Hendrix said,
I’m the one who has to die when it’s time for me to die,
and as E.M. Forster wrote in Aspects of the Novel,
Neither memory nor anticipation is much interested in Father Time, and all dreamers, artists and lovers are partially delivered from his tyranny; he can kill them but he cannot secure their attention, and at the very moment of doom, when the clock collected in the tower its strength and struck, they may be looking the other way.
The story I tell myself about who I am, like the story you tell yourself about who you are, changes incessantly, yet my story retains certain continuities, such as the first time I saw naked that molecular biologist with the great figure.
Goldbach in Oxford
Because you are an intelligent monkey of refined taste, oh my best beloved, you were, like me, a fan of the television series Inspector Morse, based on the novels of Colin Dexter. In those novels the eponymous inspector has a sidekick known as Sergeant Lewis. I only recently — after I had finished reading Uncle Petros, in fact — discovered that Lewis had a series of his own. Wikipedia:
Reputation is the pilot episode of Lewis. It first aired on 29 January 2006.
Synopsis
DI Lewis returns to Oxford after two years' absence and is reluctantly assigned by his new boss, DCS Innocent, to the murder of an Oxford mathematics student who was shot while participating in a sleep study.
Can you guess which problem the murdered mathematics student was working on? Of course you can.
Uncle Petros in New Orleans
Michelle Blouin Williams (who I theorize but cannot prove is no relation to the poet William Carlos Williams) is a math teacher at St. Mary’s Academy in New Orleans. Two years ago she announced that she had established a challenge with cash prize of $500 for any student who could devise a trigonometric proof of the pythagorean theorem. That’s why Ne'Kiya Jackson and Calcea Johnson worked so hard on their proof for two solid months — an eternity in teenager time: to win that $500.
Like Uncle Petros, Ms. Williams did not bother telling the students of St. Mary’s Academy that finding a proof that would satisfy her challenge was thought to be impossible. From that ‘60 Minutes’ piece:
Bill Whitaker: And did you think anyone would solve it? Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't— Bill Whitaker: What were you looking for? Michelle Blouin Williams: I was just looking for some ingenuity.
Watching that show about St. Mary’s Academy, that all-girl Catholic school in New Orleans brought back a lot of memories of my own high school experience at Jesuit/ROTC Xavier High School in New York City. I wrote about that, among other things, in my essay Catholicism and Human Sexual Response. There was a lot — an awful lot — that I did not like about Xavier High School. But I’ll say this about the Jesuits of Xavier: they, like the nuns of St. Mary’s, demanded and expected the best out of every student. They set before us any number of challenges without telling us that finding a solution was thought to be impossible.
Variations on a theme by Stephen Crane
Because you, my best beloved rando, have now read my essay I Saw a Tangerine Sun Suspended in Haze Over the Cemetery Tonight, featuring this awesome photo by Nancy Jephcote, you will appreciate this next bit.

Having read that essay, you are now familiar the origin of the poetic meme Variations on a Theme By William Carlos Williams, that one with the opening line ‘This is just to say. . .’
As I conclusively proved in my Tangerine essay, that ‘Variations’ meme was originated by the poet Kenneth Koch, and published in his Thank You and Other Poems, in 1962.

We will now take Koch’s whimsical frolic as a point of departure, much as Jackson and Johnson’s proof has been taken as a point of departure for elaborations on their insight.
In the Living Room
In the living room
I saw a creature, matrimonial, bestial,
Who, sitting on the couch,
Held my substack in her hands,
And read of it.
I said, “Is it good, friend?”
“It is bitter—bitter,” she answered;
“But it's OK, I guess
“I'll let you know,
“If I finish reading it.”In the Automobile
In the automobile
I saw a creature, female, preoccupied
Who, sitting in the shotgun seat
Looked out the window,
And said nothing.
I said, “What do you see, friend?”
“ ” she answered;
And I drove
As she ignored my existenceIn the Apartment
In the apartment
I saw a creature, scientist, naked
Who, standing at the foot of the bed
Looked fifty years into the future
She said, “Why do you persist in this foolishness? Don't you know we're old now?”
“No particular reason,” I answered;
But I like to
Because you are a babe
And because you are my wifeI was planning to use these variations to prove a theorem about the nature of time, logic, memory, photographs, nakedness, finality, unknowability, art (literature in particular), waffle cones, Catholicism & ontology, Inspector Morse and biodigital technopotheosis, but, alas, there is no room in this margin, so I will have to get to it at some other time.
‘[T]angentially related to trigonometry.’ That’s a joke.









And I thought "Gödel, Escher, Bach" was labyrinthine. Great essay, one of your finest. And given the poetry you covered reminded me of what may be my favorite poem of all time:
This Be The Verse
By Philip Larkin
-
They fuck you up, your mum and dad.
They may not mean to, but they do.
They fill you with the faults they had
And add some extra, just for you.
-
But they were fucked up in their turn
By fools in old-style hats and coats,
Who half the time were soppy-stern
And half at one another’s throats.
-
Man hands on misery to man.
It deepens like a coastal shelf.
Get out as early as you can,
And don’t have any kids yourself.
Life is an experimental journey undertaken involuntarily. -- Fernando Pessoa